- | Government Spending Government Spending
- | Working Papers Working Papers
- |
Macroeconomic Effects from Government Purchases and Taxes
The empirical evidence on the response of real GDP and other economic aggregates to changes in government purchases and taxes is thin. Particularly troubling in the existing literature is the basis
The global recession and financial crisis of 2008-09 have focused attention on fiscal stimulus packages. These packages often emphasize heightened government purchases, predicated on the view that expenditure multipliers are greater than one. The packages typically also include tax reductions, designed partly to boost disposable income and consumption (through wealth effects) and partly to stimulate work effort, production, and investment by lowering marginal incometax rates (through substitution effects).
The empirical evidence on the response of real GDP and other economic aggregates to changes in government purchases and taxes is thin. Particularly troubling in the existing literature is the basis for identification in isolating effects of changes in government purchases or tax revenue on economic activity.
This study uses longterm U.S. macroeconomic data to contribute to existing evidence along several dimensions. Spending multipliers are identified primarily from variations in defense spending, especially changes associated with buildups and aftermaths of wars. The defense news variable constructed by Ramey (2009b) allows us to distinguish temporary from permanent changes in defense spending. Tax effects are estimated mainly from changes in a newly constructed time series on average marginal income tax rates from federal and state income taxes and the social security payroll tax. Parts of the analysis differentiate substitution effects due to changes in marginal tax rates from wealth effects due to changes in tax revenue.
Section I discusses the U.S. data on government purchases since 1914, with stress on the differing behavior of defense and nondefense purchases. The variations up and down in defense outlays are particularly dramatic for World War II, World War I, and the Korean War. Section II describes the newly updated time series from 1913 to 2006 on average marginal income tax rates from federal and state individual income taxes and the social security payroll tax. Section III discusses Ramey's (2009b) defense news variable. Section IV describes the Romer and Romer (2008) measure of "exogenous" changes in federal tax revenue. Section V describes our conceptual framework for assessing effects on GDP from changes in government purchases, taxes, and other variables. Section VI presents our empirical findings. The main analysis covers annual data ending in 2006 and starting in 1950, 1939, 1930, or 1917. Section VII summarizes the principal findings and suggests avenues for additional research, particularly applications to other countries.
I. The U.S. History of Government Purchases: Defense and Nondefense
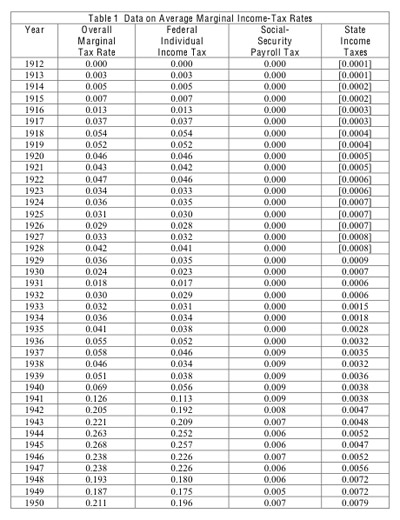
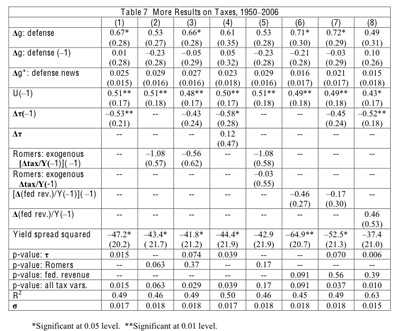
Figure 1 shows annual changes since 1914 in per capita real defense or nondefense purchases (nominal outlays divided by the GDP deflator), expressed as ratios to the previous year's per capita real GDP.1 The underlying data on government purchases are from the Bureau of Economic Analysis (BEA) since 1929 and, before that, from Kendrick (1961).2 The data on defense spending apply to the federal government, whereas those for nondefense purchases pertain to all levels of government. Our main analysis considers government spending on goods and services, not transfers or interest payments. To get a long time series, we are forced to use annual data because reliable quarterly figures are available only since 1947. The restriction to annual data avoids issues concerning seasonal adjustment.
The blue graph in Figure 1 shows the dominance of war related variations in the defense spending variable. For World War II, the value is 10.6% of GDP in 1941, 25.8% in 1942, 17.2% in 1943, and 3.6% in 1944, followed by two negative values of large magnitude, 7.1% in 1945 and 25.8% in 1946. Thus, World War II provides an excellent opportunity to estimate the government purchases multiplier; that is, the effect of a change in government purchases on GDP. The favorable factors are:
The principal changes in defense spending associated with World War II are plausibly exogenous with respect to GDP. (We neglect a possible linkage between economic conditions and war probability.)
The changes in defense spending are very large and include sharply positive and negative values.
Unlike many countries that experienced major decreases in real GDP during World War II (Barro and Ursua [2008, Table 7]), the United States did not have massive destruction of physical capital and suffered from only moderate loss of life. Hence, demand effects from defense spending should be dominant in the U.S. data. Because the unemployment rate in 1940 was still high, 9.4%, but then fell to a low of 1.0% in 1944, there is information on how the size of the defensespending multiplier depends on the amount of slack in the economy.
The U.S. time series contains two other war related cases of large, shortterm changes in defense spending. In World War I, the defense spending variable (blue graph in Figure 1) equaled 3.5% in 1917 and 14.9% in 1918, followed by 7.9% in 1919 and -8.2% in 1920. In the Korean War, the values were 5.6% in 1951, 3.3% in 1952, and 0.5% in 1953, followed by 2.1% in 1954. As in World War II, the United States did not experience much destruction of physical capital and incurred only moderate loss of life during these wars. Moreover, the changes in defense outlays would again be mainly exogenous with respect to GDP.
In comparison to these three large wars, the post 1954 period features much more modest variations in defense spending. The largest values-1.2% in 1966 and 1.1% in 1967-apply to the early part of the Vietnam War. These values are much smaller than those for the Korean War; moreover, after 1967, the values during the Vietnam War become negligible (0.2% in 1968 and negative for 1969-71). After the end of the Vietnam conflict, the largest values of the defense spending variable are 0.4-0.5% from 1982 to 1985 during the "Reagan defense buildup" and 0.3-0.4% in 2002-2004 during the post 2001 conflicts under George W. Bush. It seems unlikely that there is enough information in the variations in defense outlays after 1954 to get an accurate reading on the defense spending multiplier.
The red graph in Figure 1 shows the movements in nondefense government purchases. Note the values of 2.4% in 1934 and 2.5% in 1936, associated with the New Deal. Otherwise, the only clear pattern is that nondefense purchases decline during major wars and rise in the aftermaths of these wars. For example, the nondefense purchases variable ranged from -1.0% to -1.2% between 1940 and 1943 and from 0.8% to 1.6% from 1946 to 1949. It is hard to be optimistic about using the macroeconomic time series to isolate multipliers for nondefense purchases. The first problem is that the variations are small compared to those in defense outlays. More importantly, the changes in nondefense purchases are likely to be endogenous with respect to GDP. That is, fluctuations in the overall economy likely induce governments, especially at the state and local levels, to spend more or less on goods and services. As Ramey (2009a, pp. 5-6) observes, outlays by state and local governments have been the dominant part of nondefense government purchases (since at least 1929). These expenditures-which relate particularly to education, public order, and transportation-likely respond to variations in state and local revenue caused by changes in aggregate economic conditions. Whereas war and peace is a plausible exogenous driver of defense spending, we lack similarly convincing exogenous changes in nondefense purchases.
A common approach in the empirical literature, exemplified by Fair (2010) and Blanchard and Perotti (2002), is to include government purchases in a large macroeconometric model or vectorautoregression (VAR) system and then make identifying assumptions concerning exogeneity and timing. Typically, the government purchases variable is assumed to move first, so that the contemporaneous associations with GDP and other macroeconomic aggregates are treated as causal influences from government purchases to the macro variables. This approach seems satisfactory for wardriven defense spending but is problematic for other forms of government expenditures.
II. Ramey's Defense-News Variable
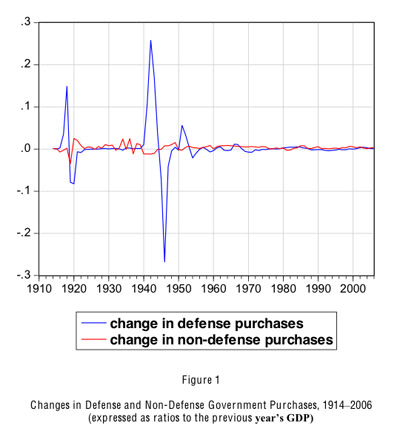
The data already discussed refer to actual defense spending (blue graph in Figure 1). For our macroeconomic analysis, we would like to compare current spending with prospective future spending and, thereby, assess the perceived degree of permanence of current spending. For example, in the prelude to the U.S. entrance into World War II in 1939-40, people may have increasingly believed that future defense outlays would rise because of the heightened chance that the United States would enter the war. In contrast, late in the war, 1944-45, people may have increasingly thought that the war would end-successfully for the United States-and, hence, that future defense outlays would fall.
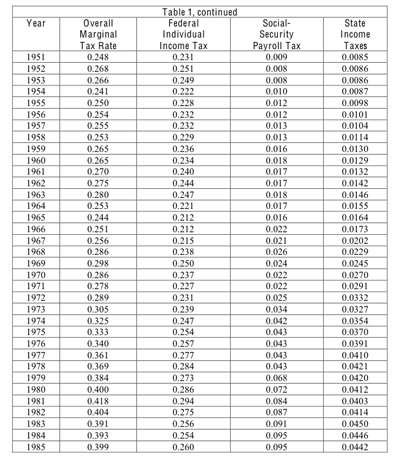
Ramey (2009b) quantified these notions about anticipated future defense expenditures from 1939 to 2008. She measured these expectations by using news sources, primarily articles in Business Week, to estimate the present discounted value of expected changes in defense spending during quarters of each year. She considered changed expectations of nominal outlays in most cases over the next three to five years, and she expressed these changes as present values by using U.S. Treasury bond yields. As an example, she found (Ramey [2009b, p.8]) that, during the second quarter of 1940, planned nominal defense spending rose by $3 billion for 1941 and around $10 billion for each of 1942, 1943, and 1944. Using an interest rate of 2.4%, she calculated for 1940.2 that the present value of the changed future nominal spending was $31.6 billion—34% of 1939's nominal GDP.
Ramey (2009a, Table 2) provides quarterly data, which we summed for each year to construct an annual variable beginning in 1939. The starting date of 1939 is satisfactory for most of our analysis. To go back further, we assumed, first, that the defense news variable was zero from 1921 to 1938 (a reasonable approximation given the absence of U.S. wars and the low and reasonably stable ratio of defense spending to GDP in this period). For World War I (1914-20), we assumed that the overall increment to expected future real spending coincided with the total increment to actual real spending, compared to the baseline value from 1913 (for which we assumed the defensenews variable equaled zero). Then we assumed that the timing of the news corresponded to the one found by Ramey (2009a, Table 2) for World War II: runup period for 1914-16 corresponding to 1939-40, war buildup of 1917-18 corresponding to 1941-43, and wind down for 1919-20 corresponding to 1944-46. The resulting measure of defense news for World War I is a rough approximation, and it would be valuable to extend Ramey's analysis formally to this period.
Figure 2 shows the estimates for the present value of the expected addition to nominal defense spending when expressed as a ratio to the prior year's nominal GDP. World War II stands out, including the runup values of 0.40 in 1940, 1.46 in 1941, and 0.75 in 1942, and the winddown values of -0.07 in 1944 and -0.19 in 1945. The peak at the start of the Korean War (1.16 in 1950) is impressive, signaling that people were concerned about the potential start of World War III. The peak values for World War I are comparatively mild, at 0.20 for 1917-18, but this construction involves a lot of assumptions.
III. Average Marginal Income-Tax Rates
Marginal income-tax rates have substitution effects that influence decisions on work versus consumption, the timing of consumption, investment, capacity utilization, and so on. Therefore, we expect changes in these marginal tax rates to influence GDP and other macroeconomic aggregates. To gauge these effects at the aggregate level, we need measures of average marginal income-tax rates, AMTR—or other gauges of the distribution of marginal tax rates across economic agents.
Barro and Sahasakul (1983, 1986) used the Internal Revenue Service (IRS) publication Statistics of Income, Individual Income Taxes from various years to construct average marginal tax rates from the U.S. federal individual income tax from 1916 to 1983.3 The Barro-Sahasakul series that we use weights each individual marginal income tax rate by adjusted gross income or by analogous income measures available before 1944. The series takes account of non-filers, who were numerous before World War II. The 1986 study added the marginal income-tax rate from the social security (FICA) tax on wages and self-employment income (starting in 1937 for the main socialsecurity program and 1966 for Medicare). The analysis considered payments by employers, employees, and the self-employed and took account of the zero marginal tax rate for social security, but not Medicare, above each year's income ceiling. The earlier analysis and our present study do not allow for offsetting individual benefits at the margin from making social security "contributions".
We use the National Bureau of Economic Research (NBER) TAXSIM program, administered by Dan Feenberg, to update the Barro-Sahasakul data. TAXSIM allows for the increasing complexity of the federal individual income tax due to the alternative minimum tax, the earned-income tax credit (EITC), phase-outs of exemptions and deductions, and so on.4 TAXSIM allows for the calculation of average marginal income-tax rates weighted in various ways-we focus on the average weighted by a concept of income that is close to labor income: wages, self-employment income, partnership income, and S-corporation income. Although this concept differs from the adjusted-gross-income measure used before (particularly by excluding most forms of capital income),5 we find in the overlap from 1966 to 1983 that the Barro-Sahasakul and NBER TAXSIM series are highly correlated in terms of levels and changes. For the AMTR from the federal individual income tax, the correlations from 1966 to 1983 are 0.99 in levels and 0.87 in first differences. For the social-security tax, the correlations are 0.98 in levels and 0.77 in first differences. In addition, at the start of the overlap period in 1966, the levels of Barro-Sahasakul—0.217 for the federal income tax and 0.028 for social security—are not too different from those for TAXSIM—0.212 for the federal income tax and 0.022 for social security. Therefore, we are comfortable in using a merged series to cover 1912 to 2006. The merged data use the Barro-Sahasakul numbers up to 1965 (supplemented, as indicated in note 3, for 1913-15) and the new values from 1966 on.
The new construct adds average marginal income-tax rates from state income taxes.6 From 1979 to 2006, the samples of income-tax returns provided by the IRS to the NBER include state identifiers for returns with AGI under $200,000. Therefore, with approximations for allocating high-income tax returns by state, we were able to use TAXSIM to compute the AMTR from state income taxes since 1979. From 1929 to 1978, we used IncTaxCalc, a program created by Jon Bakija, to estimate marginal tax rates from state income taxes. To make these calculations, we combined information on each state's tax code (incorporated into IncTaxCalc) with estimated numbers on the distribution of income levels by state for each year. The latter estimates used BEA data on per capita state personal income.7 The computations take into account that, for people who itemize deductions, an increase in state income taxes reduces federal income-tax liabilities.
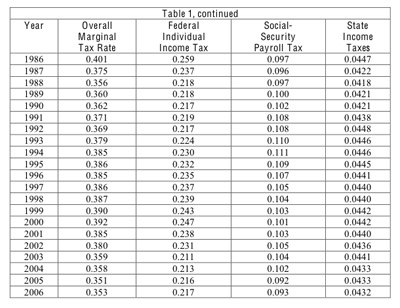
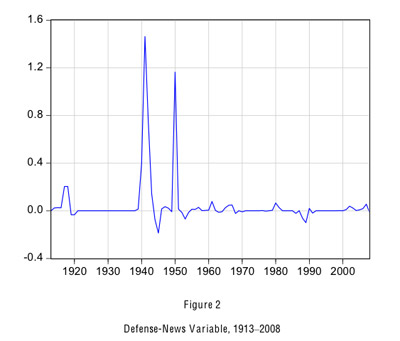
Table 1 and Figure 3 show our time series from 1912 to 2006 for the overall average marginal-income tax rate and its three components: the federal individual income tax, social security payroll tax (FICA), and state income taxes. In 2006, the overall AMTR was 35.3%, breaking down into 21.7% for the federal individual income tax, 9.3% for the social-security levy (inclusive of employee and employer parts), and 4.3% for state income taxes.8 For year-to-year changes, the movements in the federal individual income tax usually dominate the variations in the overall marginal rate. However, rising social-security tax rates were important from 1971 to 1991. Note that, unlike for government purchases, the marginal income-tax rate for each household really is an annual variable; that is, the same rate applies at the margin to income accruing at any point within a calendar year. Thus, for marginal tax-rate variables, it would not be meaningful to include variations at a quarterly frequency.9
Given the focus on wage and related forms of income, our constructed average marginal income-tax rate applies most clearly to the labor-leisure margin. However, unmeasured forms of marginal tax rates (associated with corporate income taxes, sales and property taxes, means- testing for transfer programs, and so on) might move in ways correlated with the measured AMTR.
Many increases in the AMTR from the federal income tax involve wartime, including WWII (a rise in the rate from 3.8% in 1939 to 25.7% in 1945, reflecting particularly the extension of the income tax to most households), WWI (an increase from 0.6% in 1914 to 5.4% in 1918), the Korean War (going from 17.5% in 1949 to 25.1% in 1952), and the Vietnam War (where "surcharges" contributed to the rise in the rate from 21.5% in 1967 to 25.0% in 1969). The AMTR tended to fall during war aftermaths, including the declines from 25.7% in 1945 to 17.5% in 1949, 5.4% in 1918 to 2.8% in 1926, and 25.1% in 1952 to 22.2% in 1954. No such reductions applied after the Vietnam War. A period of rising federal income-tax rates prevailed from 1971 to 1978, with the AMTR from the federal income tax increasing from 22.7% to 28.4%. This increase reflected the shifting of households into higher rate brackets due to high inflation in the context of an un-indexed tax system. Comparatively small tax-rate hikes include the Clinton increase from 21.7% in 1992 to 23.0% in 1994 (and 24.7% in 2000) and the rise under George H.W. Bush from 21.7% in 1990 to 21.9% in 1991. Given the hype about Bush's violation of his famous pledge, "read my lips, no new taxes" it is surprising that the AMTR rose by only two-tenths of a percentage point in 1991.
Major cuts in the AMTR from the federal income tax occurred under Reagan (25.9% in 1986 to 21.8% in 1988 and 29.4% in 1981 to 25.6% in 1983), George W. Bush (24.7% in 2000 to 21.1% in 2003), Kennedy-Johnson (24.7% in 1963 to 21.2% in 1965), and Nixon (25.0% in 1969 to 22.7% in 1971, reflecting the introduction of the maximum marginal rate of 60% on earned income).
During the Great Depression, the AMTR from federal income taxes fell from 4.1% in 1928 to 1.7% in 1931, mainly because falling incomes within a given tax structure pushed people into lower rate brackets. Then, particularly because of attempts to balance the federal budget by raising taxes under Hoover and Roosevelt, the AMTR rose to 5.2% in 1936.
Although social-security tax rates have less high-frequency variation, they sometimes increased sharply. The AMTR from social security did not change greatly from its original value of 0.9% in 1937 until the mid 1950s but then rose to 2.2% in 1966. The most noteworthy period of rising average marginal rates is from 1971—when it was still 2.2%—until 1991, when it reached 10.8%. Subsequently, the AMTR remained reasonably stable, though it fell from 10.2% in 2004 to 9.3% in 2006 (due to rising incomes above the social-security ceiling).
The marginal rate from state income taxes rose from less than 1% up to 1956 to 4.1% in 1977 and has since been reasonably stable. We have concerns about the accuracy of this series, particularly before 1979, because of missing information about the distribution of incomes by state. However, the small contribution of state income taxes to the overall AMTR suggests that this measurement error would not matter a lot for our main findings. The results that we report later based on the overall AMTR turn out to be virtually unchanged if we eliminate state income taxes from the calculation of the overall marginal rate.
IV. Romer-Romer Exogenous Tax-Change Variable
Romer and Romer (2008, Table 1) use a narrative approach, based on congressional reports and other sources, to assess all significant federal tax legislation from 1945 to 2007. Their main variable (columns 1-4) gauges each tax change by the size and timing of the intended effect on federal tax revenue during the first year in which the tax change takes effect. In contrast to the marginal income-tax rates discussed before, the Romer-Romer focus is on income effects related to the federal government's tax revenue. In practice, however, their tax-change series has a high positive correlation with shifts in marginal income-tax rates; that is, a rise in their measure of intended federal receipts (expressed as a ratio to the previous year's GDP) usually goes along with an increase in the AMTR, and vice versa.10 Consequently, the Romer-Romer or AMTR variable used alone would pick up a combination of wealth and substitution effects. However, when we include the two tax measures together, we can reasonably view the Romer-Romer variable as isolating wealth effects,11 with the AMTR variable capturing substitution effects.12
Because the Romer-Romer variable relates to planned changes in federal tax revenue, assessed during the prior legislative process, this measure avoids the contemporaneous endogeneity of tax revenue with respect to GDP. Thus, the major remaining concern about endogeneity involves politics; tax legislation often involves feedback from past or prospective economic developments. To deal with this concern, Romer and Romer divide each tax bill (or parts of bills) into four bins, depending on what the narrative evidence reveals about the underlying motivation for the tax change. The four categories are (Romer and Romer [2008, "...responding to a current or planned change in government spending, off-setting other influences on economic activity, reducing an inherited budget deficit, and attempting to increase long-run growth." They classify the first two bins as endogenous and the second two as exogenous, although these designations can be questioned.13 In any event, we use the Romer-Romer "exogenous" tax-revenue changes to form an instrument for changes in the AMTR or for changes in overall federal revenue. Romer and Romer (2008, Table 1, columns 1-4) provide quarterly data, but we use these data only at an annual frequency, thus conforming to our treatment for government purchases and average marginal income-tax rates.
V. Framework for the Analysis
Economists have surely not settled on a definitive theoretical model to assess macroeconomic effects of government purchases and taxes. To form a simple empirical framework, we get guidance from the neoclassical setting described in Barro and King (1984). Central features of this model are a representative agent with time-separable preferences over consumption and leisure, an assumption that consumption and leisure are both normal goods, and "market clearing." The baseline model also assumes a closed economy, the absence of durable goods, and lump-sum taxation.
In the baseline model, pure wealth effects—for example, changes in expected future government purchases—have no impact on current GDP. The reason is that—with time-separable preferences, an absence of durable goods, and a closed economy—equilibrium choices of work effort and consumption are divorced from future events. This result means that temporary and permanent changes in government purchases have the same effect on GDP. An increase in purchases raises GDP because consumption and leisure decline, and the fall in leisure corresponds to a rise in labor input. The spending multiplier is less than one; that is, GDP rises by less than the increase in government purchases.
With durable goods, a temporary increase in government purchases reduces current investment, thereby mitigating the decreases in consumption and leisure. The spending multiplier is still less than one. Wealth effects now matter in equilibrium: if the increase in purchases is perceived as more permanent, the negative wealth effect is larger in magnitude, and the declines in consumption and leisure are greater. Therefore, the positive effect on GDP from a given-size expansion of government purchases is larger the more permanent the change. However, an allowance for variable capital utilization can offset this conclusion. Utilization tends to expand more when the increase in purchases is more temporary—because higher utilization (which raises output at the expense of higher depreciation of capital) is akin to reduced investment.
International openness is analogous to variable domestic investment. A temporary rise in government purchases leads to a current-account deficit; that is, net foreign investment moves downward along with domestic investment. The response of the current account mitigates the adjustments of consumption, leisure, and domestic investment. However, the current-account movements arise only when government purchases in the home economy change compared to those in foreign economies, a condition that may not hold during a world war. War may also compromise the workings of international asset markets and, thereby, attenuate the responses of the current account to changes in defense spending.
In the baseline model, variations in lump-sum taxes have no effects in equilibrium. More generally, changes in lump-sum taxes may have wealth effects involving signals about future government purchases. However, if a decrease in lump-sum taxes has a positive wealth effect, it reduces current GDP—because consumption and leisure increase, implying a fall in labor input.
An increase in today's marginal tax rate on labor income reduces consumption and raises leisure, thereby lowering labor input and GDP. In the closed-economy setting without durable goods, changes in expected future marginal tax rates do not affect current choices in equilibrium. With durable goods, a rise in the expected future tax rate on labor income affects current allocations in the same way as a negative wealth effect. That is, consumption and leisure decline, and labor input and GDP increase. Therefore, a temporary rise in the marginal tax rate on labor income has more of a negative effect on today's GDP than an equal-size, but permanent, increase in the tax rate.
To assess empirically the effects of fiscal variables on GDP, we estimate annual equations for the growth rate of per capita real GDP of the form:
(1) (yt - yt-1/yt-1 = β0 + β1(gt - gt-1)/yt-1 + β2(g*t - g*t-1)/yt-1 + β3(τt - τt-1) + other variables
In the equation, yt is per capita real GDP for year t, gt is per capita real government purchases for year t, g*t is a measure of expected future real government purchases as gauged in year t, τtis the average marginal income-tax rate for year t.
The form of equation (1) implies that the coefficient β is the multiplier for government purchases; that is, the effect on year t's GDP from a one unit increase in purchases for given values of the other right-side variables.14 If the variable g*t holds fixed expected future government purchases, then β1 represents the contemporaneous effect on GDP from temporary purchases. We are paticularly interested in whether β1 is greater than zero, greater than one, and larger when the economy has more slack (as implied by some models). We gauge the last effect by adding to the equation an interaction between the variable (gt - gt-1)/yt-1 and the lagged unemployment rate, Ut-1, an indicator of the amount of slack in the economy.
We emphasize results where gt in equation (1) corresponds to defense spending, and the main analysis includes the same variable on the instrument list; that is, we treat variations in defense spending as exogenous with respect to changes in GDP. We also explore an alternative specification that treats only war-related movements in defense spending as exogenous; that is, the gt variable interacted with a dummy for years related to major war. Since the main movements in defense spending are war related (Figure 1), we end up with similar results—especially in samples that cover WWII—as those found when the defense-spending variable is itself on the instrument list. We also consider representing gt by non-defense purchases, but this setting leads to problems because of the lack of convincing instruments.
In the underlying model, the main effect of government purchases on GDP would be contemporaneous, although lagged effects would arise from changes in the capital stock and the dynamics of adjustment costs for factor inputs. In our empirical analysis with annual data, the main effect is contemporaneous, but a statistically significant effect from the first lag of defense purchases shows up in samples that include WWII. To allow for this influence, we add to the right-hand side of equation (1) the lagged value, (gt-1 - gt-2)/yt-2.
We measure (g*t - g*t-1)/yt-1 in equation (1) by Ramey's (2009a, Table 2) defense-news variable, discussed before and shown in Figure 2. We anticipate β2>0 because of the wealth effects discussed earlier. More specifically, the Ramey variable focuses on projections of defense outlays three to five years into the future. Therefore, if people first become aware in year t of a permanent change in military outlay starting in year t, the variable g*t-g*t-1 constructed by Ramey's procedure would move by about four times the variable gt-gt-1. Hence, the full effect on year t's GDP from a "permanent" change in gt is roughly β1 + 4(β2). We do not find a statistically significant effect on GDP from the lagged value of the g* variable.
Increases in government purchases may be accompanied by increases in marginal income-tax rates, which tend to reduce GDP. According to the tax-smoothing view (Barro [1979]; Aiyagari, Marcet, Sargent, and Seppala [2002]), tax rates rise more the longer lasting the anticipated increase in government spending. Thus, on this ground, the effect of increased government purchases on GDP tends to be larger the more temporary the change (an offset to the predictions from wealth effects). However, equation (1) holds fixed changes in tax rates, represented by τt. For given tax rates, a rise in government purchases would have a larger effect on GDP the more permanent the perceived change, as gauged by the g*t variable.
Tax-smoothing considerations imply a Martingale property for marginal tax rates: future changes in tax rates would not be predictable based on information available at date t. Redlick (2009) tests this hypothesis for the data on the overall average marginal income-tax rate shown in Table 1. He finds that the Martingale property is a good first-order approximation but that some variables have small, but statistically significant, predictive content for future changes in the AMTR. Because most changes in the AMTR are close to permanent, we are unable to isolate empirically effects on GDP from temporary changes in tax rates.15
As with government purchases, the main effect of a permanent change in the marginal income-tax rate on GDP would be contemporaneous in the underlying model, although lagged effects would arise from the dynamics of changes in factor inputs. Although the marginal tax rate for each individual is an annual variable, changes in tax schedules can occur at any point within a year, and these changes are often "retroactive," in the sense of applying without proration to the full year's income. For this reason, the adjustment of GDP may apply only with a lag to the measured shifts in marginal tax rates. Therefore, we anticipate more of a lagged response of GDP to the tax rate, τt, than to government purchases, gt. In fact, it turns out empirically in annual data that the main response of the GDP change, yt - yt-1, is to the lagged tax-rate change τt-1 - τt-2. Our initial empirical analysis focuses on this lagged tax-rate change.
We make the identifying assumption that changes in average marginal income-tax rates lagged one or more years can be satisfactorily treated as pre-determined with respect to GDP. We can evaluate this assumption from the tax-smoothing perspective; as already mentioned, this approach implies that future changes in tax rates would not be predictable based on information available at date t. If tax smoothing holds as an approximation, then the change in the tax rate for year t, τt - τt-1, would reflect mainly information arriving during year t about the future path of the ratio of real government expenditure, Gt+T (inclusive here of transfer payments), to real GDP, Yt+T. Information that future government outlays would be higher in relation to GDP would increase the current tax rate. For our purposes, the key issue concerns the effects of changes in expectations about future growth rates of GDP. Under tax-smoothing, these changes would not impact the current tax rate if the shifts in expected growth rates of GDP go along with corresponding changes in expected growth rates of government spending. Thus, our identifying assumption is that any time-varying expectations about growth rates of future GDP do not translate substantially into changes in the anticipated future path of G/Y and, therefore, do not enter substantially into the determination of tax rates.
When we attempt to gauge the contemporaneous effect of the average marginal income-tax rate τt, on GDP we encounter serious identification problems: changes in τt, are surely endogenous with respect to contemporaneous GDP. We take two approaches to constructing instruments to isolate the contemporaneous effect of tax-rate changes on GDP. First, we computed the average marginal income-tax rate that would apply in year t based on incomes from year t-1. This construct eliminates the channel whereby higher income shifts people into higher tax-rate brackets for a given tax law. However, this approach leaves the likely endogeneity associated with legislative decisions about tax rates. To address the endogeneity of legislation, we use as an instrument the "exogenous" part of the Romer and Romer (2008, Table 1, columns 1-4) federal-tax-change series.
In Romer and Romer (2009), the counterpart of τt in equation (1) is the exogenous part of tax revenue collected as a share of GDP. As noted before, their approach focuses on wealth effects, rather than substitution effects. In our underlying model, an increase in tax revenue could have a negative wealth effect if it signals a rise in expected future government purchases—not fully held constant by the variable g*tin equation (1). For given tax rates, the negative wealth effect tends to raise labor input and, therefore, GDP. In other words, we predict β3> 0 in equation (1).
The other variables in equation (1) include indicators of the lagged state of the business cycle. This inclusion is important because, otherwise, the fiscal variables might reflect the dynamics of the business cycle. In the main analysis, we include the first lag of the unemployment rate, Ut-1. Given a tendency for the economy to recover from recessions, we expect a positive coefficient on Ut-1. With the inclusion of this lagged business-cycle variable, the estimated form of equation (1) does not reveal significant serial correlation in the residuals. We also considered as business-cycle indicators the first lag of the dependent variable and the deviation of the previous year's log of per capita real GDP from its "trend." However, these alternative variables turn out not to be statistically significant once Ut-1 is included.
Many additional variables could affect GDP. However, as Romer and Romer (2009) argue, omitted variables that are orthogonal to the fiscal variables (once lagged business-cycle indicators are included) would not bias the estimated effects of the fiscal variables. The main effect that seemed important to consider—particularly for samples that include the Great Depression of 1929-33—is an indicator of monetary/credit conditions. In a recent study, Gilchrist, Yankov, and Zakrajsek (2009) argue that default spreads for corporate bonds compared to similar maturity U.S. Treasury bonds have substantial predictive power for macroeconomic variables for 1990-2008. They also discuss the broader literature on the predictive power of default spreads, parts of which focus on the Great Depression (Stock and Watson [2003]).
In applying previous results on default spreads to our context, we have to rely on the available long-term data on the gap between the yield to maturity on long-maturity Baa-rated corporate bonds and that on long-maturity U.S. government bonds. This yield spread should capture distortions in credit markets, and the square of the spread (analogous to conventional distortion measures for tax rates) works in a reasonably stable way in the explanation of GDP growth in equation (1). Since the contemporaneous spread would be endogenous with respect to GDP, we instrument with the first lag of the spread variable.16 That is, given the lagged business-cycle indicator already included, we treat the lagged yield spread as pre-determined with respect to GDP. Although the inclusion of this credit variable likely improves the precision of our estimates of fiscal effects, we get similar results if the credit variable is omitted.
An additional issue for estimating equation (1) is measurement error in the right-hand- side variables, a particular concern because government purchases--which appear on the right-hand side of the equation--are also a component of GDP on the left-hand side. Consider a simplified version of equation (1):
(2) yt = β0 + β1(gt) + error term
GDP equals government purchases plus the other parts of GDP (consumer spending, gross private domestic investment, net exports). If we label these other parts as xt, we have:
(3) yt = gt + xt.
Consider estimating the equation:
(4) xt = α0 + α1(gt) + error term
where α1, if negative, gauges the crowding-out of gt on other parts of GDP. Measurement error in gt tends to bias standard estimates of α1 toward zero. However, a comparison of equation (2) with equations (3) and (4) shows that the estimate of β1 coincides with 1 + estimate of α1. Therefore, a bias in the estimate of α1 toward zero corresponds to a bias in the estimate of β1 toward one. Thus, if α1<0, spending multipliers tend to be over-estimated.
VI. Empirical Results
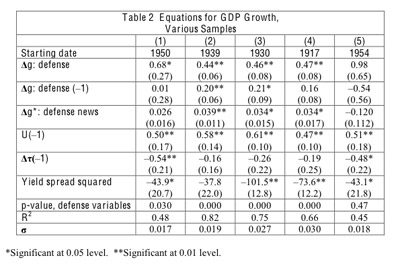
Table 2 shows regressions with annual data of the form of equation (1). The samples all end in 2006 (reflecting a lag in the availability of data on the average marginal income-tax rate). The starting year is 1950 (including the Korean War), 1939 (including WWII), 1930 (including the Great Depression), or 1917 (including WWI and the 1921 contraction). The last column, starting in 1954, excludes the main variations in defense spending.
A. Defense-Spending Multipliers
Consider the estimated coefficients on the contemporaneous defense-spending variable, Δg: defense. With the defense-news variable held fixed, the coefficient on Δg: defense gives the contemporaneous multiplier for purely temporary spending. For all samples that start in 1950 or earlier, the estimated coefficient of Δg: defense in Table 2 is significantly greater than zero at the 5% level, with p values less than 0.01 for samples that include WWII.17 For the 1950 sample, the estimated coefficient, 0.68 (s.e. = 0.27), is insignificantly different from one (p-value = 0.24). For the longer samples, the estimated coefficients are significantly less than one with p-values less than 0.01. In columns 2-4 of the table, the estimated coefficient is between 0.44 and 0.47, with standard errors between 0.06 and 0.08.18
The estimated coefficient on the lagged change in defense purchases, Δg: defense(-1), is close to zero for the 1950 sample but around 0.2 for samples that include WWII. For the 1939 sample, the estimate is 0.20 (s.e. = 0.06), which differs significantly from zero with a p-value less than 0.01. In this case, the estimated multiplier for temporary defense spending is 0.44 in the current year and 0.64 (0.44 + 0.20) when cumulated over two years. The last estimate is still significantly less than one (with a p-value of 0.000).
The estimated coefficient of the defense-news variable Δg*: defense news, is positive in samples that start in 1950 or earlier—and significantly different from zero with a p-value less than 0.05 for the longer samples.19 Recall that this variable gives the effect on year t's GDP from a change the same year in the expected present value of future defense spending. As examples, 1940 and 1950 were years with lots of news about coming defense buildups. The positive coefficient on the news variable accords with the model's prediction, whereby the negative wealth effect from greater prospective defense spending leads to more work effort and, hence, higher GDP. In contrast, in usual Keynesian models, the negative wealth effect reduces consumer demand and leads to lower GDP, the opposite of the empirical pattern.
As discussed before, for a permanent increase in defense spending that starts and becomes recognized in year t, the full multiplier on current GDP equals the coefficient of Δg: defense plus roughly four times the coefficient of Δg*: defense news (because Ramey's defense-news variable applies three-to-five years into the future). For example, for the 1939 sample in column 2 of Table 2, the point estimate of this full multiplier is about 0.44 + 4*0.039 = 0.60. To put it another way, 4*0.039 = 0.16 gives the excess of the contemporaneous multiplier for permanent spending over that for temporary spending. The estimated multiplier for a permanent increase in spending, 0.60, is still significantly less than one (with a p-value of 0.000). The estimated multiplier over two years for a permanent change in defense spending is 0.60 plus 0.20 (the estimated coefficient on &Deltag: defense(-1) in column 2), or around 0.80. This estimate is still significantly less than one (with a p-value of 0.004).
As discussed before, each regression includes the lagged unemployment rate, Ut-1, to pick up business-cycle dynamics. The estimated coefficients on Ut-1 in Table 2 are significantly positive with p-values less than 0.01, indicating a tendency for the economy to recover by growing faster when the lagged unemployment rate is higher. We also tried as business-cycle variables the lag of the dependent variable and the lag of the deviation of the log of per capita GDP from its trend (gauged by a one-sided Hodrick-Prescott filter). In all cases, the estimated coefficients of these alternative variables differed insignificantly from zero, whereas the estimated coefficient on the lagged unemployment rate remained significantly positive.
We added an interaction term, (Δg: defense)*Ut-1 to assess whether the contemporaneous defense-spending multiplier depends on the amount of slack in the economy, gauged by the lagged unemployment rate. The variable Ut-1 in this interaction term enters as a deviation from the median unemployment rate of 0.0557 (calculated from 1914 to 2006). In this specification, the coefficient on the variable Δg: defense reveals the multiplier for temporary defense spending when the lagged unemployment rate is at its median, and the interaction term indicates how this multiplier varies as Ut-1 deviates from its median.
The estimated coefficient of the interaction variable, (Δg: defense)*Ut-1, differs insignificantly from zero for each sample considered in Table 2. For example, if we add this variable to the 1939 regression (column 2), the estimated coefficient is 0.6 (s.e. = 2.6), and the estimated coefficients and standard errors for the other variables remain similar to those shown in the table. In previous research, which did not consider the defense-news variable, the multiplier appeared to rise with the unemployment rate. For the 1939 sample (column 2), if we delete the defense-news variable and add the interaction term, the estimated coefficient of the interaction variable is 4.8 (2.1). This coefficient would imply that a rise in the unemployment rate by two percentages points increases the contemporaneous multiplier by about 0.1. The reason that the inclusion of the defense-news variable eliminates this effect is that the interaction variable is particularly large in the run-up to World War II, reflecting the unemployment rate of 9.4% in 1940. However, the defense-news variable is also large at this time—once the effect from this variable is taken into account, the interaction term is no longer important. Further,when Δg*: defense news and the interaction term are included together for the 1939 sample, estimated coefficient of the news variable is significantly positive, 0.037 (s.e. = 0.014), whereas that for the interaction is insignificantly different from zero, 0.6 (2.6).
As already noted, the wartime experiences include substantially positive and negative values for Δg: defense (and also for Δg*: defense news). The estimates shown in Table 2 assume that the effects on GDP are the same for increases and decreases in spending, notably, for war buildups and demobilizations. Tests of this hypothesis are accepted at high p-values. For example, for the 1939 sample (Table 2, column 2), the estimated coefficients are 0.50 (s.e. = 0.09) for positive values of Δg: defense and 0.39 (0.08) for negative values, with a p-value of 0.40 for a test of equal coefficients. We can also allow for separate coefficients for positive and negative values of the lagged defense-spending variable. In this case, for contemporaneous --: defense, we get 0.40 (0.11) for positive values and 0.41 (0.08) for negative values, whereas for lagged Δg: defense, we get 0.33 (0.10) for positive values and 0.12 (0.08) for negative values. The p-value for a test that the coefficients of the positive and negative values are the same in both pairs is 0.18. We also accept the hypothesis (with a p-value of 0.20) when broadened to include positive versus negative values of Δg*: defense news. Thus, the evidence accords with the condition that spending multipliers are the same for increases and decreases in defense spending.
The estimates in Table 2 treat all variations in defense spending as exogenous. However, the case for exogeneity with respect to GDP is most compelling for variations in defense spending associated with buildups and wind-downs of major wars. In practice, because the wartime observations capture the principal fluctuations in defense spending, the results change little if we modify the instrument list to exclude Δg: defense but to include this variable interacted with "war years".20 For the 1950 sample, the estimated coefficient on Δg: defense becomes 0.86 (s.e. = 0.30), somewhat higher than the one in Table 2, column 1; that on Δg: defense (-1) becomes -0.05 (0.28); and that on Δg*: defense news is still 0.026 (0.016). For samples that start in 1939 or earlier, the change in the instrument list has a negligible impact.21 For example, for the 1939 sample in column 2, the estimated coefficient on Δg: defense becomes 0.46 (s.e. = 0.06), that on Δg: defense (-1) becomes 0.19 (0.06), and that on Δg*: becomes 0.038 (0.011).
For a sample that starts after the Korean War, 1954-2006 in column 5 of Table 2, the point estimates of the coefficients are 0.98 (s.e.=0.65) on Δg: defense and and -.54 (0.56) on Δg: defense (-1). The high standard errors imply that neither estimated coefficient, nor the two jointly, differs significantly from zero. The sum of the two coefficients also differs insignificantly from one. For the variable Δg*: defense news, the result is -0.12 (0.11); that is, the large standard error makes it impossible to draw meaningful inferences. The estimated coefficients of the other variables are close to those for the 1950 sample in column 1. The conclusion is that, in the post-1954 sample, there is insufficient variation in defense outlays to get an accurate reading on defense-spending multipliers.
B. Marginal Income-Tax Rates
The equations in Table 2 include the lagged change in the average marginal income-tax rate, Δτ(-1). For the sample that starts in 1950, in column 1, the estimated coefficient is -0.54 (s.e. = 0.21), which is significantly negative with a p-value less than 0.01. Thus, the estimate is that a cut in the AMTR by 1 percentage point raises next year's per captia GDP by around 0.5%.
We can compare our estimated effect of tax-rate changes on GDP to microeconomic estimates of labor-supply elasticities, as summarized by Chetty (2009, Table 1). His results apply to elasticities of hours or taxable income with respect to 1-τ, where τ is the marginal income-tax rate. For 17 studies (excluding those based on macroeconomic data), the mean of the estimated elasticities, η, is 0.33. The implied effect of a change in τ on the log of hours or taxable income entails multiplying η by -1/(1-τ). If we evaluate this expression at the sample mean for our AMTR from 1950 to 2006 (which happens also to be 0.33), we get that the effect of a change in τ hours or taxable income is -η/(1-τ) = 0.33(1.49) = -0.49. If GDP moves in the same proportion as hours and taxable income, this number should correspond to the estimated coefficient on Δτ(-1) in Table 2. Since that point estimate is -0.54, there does turn out to be a close correspondence. That is, our macroeconomic estimate of the response of GDP to a change in the AMTR accords with typical microeconomic estimates of labor-supply elasticities.
The estimated coefficient of -0.54 Δτ(-1) in Table 2, column 1, does not correspond to a usual tax multiplier for GDP. Our results connect the change in GDP to a shift in the average marginal income-tax rate, not to variations in tax revenue, per se. As an example, for a revenue-neutral change in the tax-rate structure, such as the plan for the 1986 tax reform, the conventional tax multiplier would be minus infinity. However, the typical pattern (reasonable from the perspective of optimal taxation) is that increases in the ratio of tax revenue to GDP accompany increases in the AMTR, and vice versa. We can, therefore, compute a tax multiplier that gives the ratio of the change in GDP to the change in tax revenue when we consider the typical relation of tax revenue to the AMTR.
Let T be the average tax rate, gauged by the ratio of federal revenue to GDP, so that real revenue is Τ(GDP). The change in revenue, when expressed as a ratio to GDP, is:
(5) Δ(revenue)/GDP = Τ(ΔGDP)/GDP + ΔΤ.
The estimates in Table 2, column 1, suggest ΔGDP/GDP = -0.54(Δτ) marginal income-tax rate (applying here to federal taxes).
We now have to connect the change in the average tax rate, ΔΤ, to Δτ. From 1950 to 2006, the average of Τ (nominal federal revenue divided by nominal GDP) is 0.182. The average for τ (based only on the federal individual income tax plus social security) is 0.297. We therefore take as a typical relation that an increase in τ by one percentage point associates with an increase in Τ by 0.61 of a percentage point (the ratio of 0.182 to 0.297). If we substitute this result and the previous one for ΔGDP/GDP into equation (5), we get
(6) Δ(revenue)/GDP = (0.54(Τ) + 0.61)Δτ.
If we evaluate equation (6) at the sample average for Τ of 0.182, we get
(7) Δ(revenue)/GDP = 0.51(Δτ)
Finally, we get that the "tax multiplier" is
(8) ΔGDP/Δ(revenue) = [ΔGDP/GDP]/Δ(revenue)/GDP]
Hence, the empirical results correspond to a conventional tax multiplier of around -1.1.
We found in Table 2, for given average marginal income-tax rates, that the estimated defense-spending multipliers ranged from 0.4 to 0.8, depending on whether we considered effects contemporaneously or over two years and whether the change in spending was temporary or permanent. These spending multipliers pertain most clearly to variations in defense spending that are deficit financed. If, instead, higher spending goes along with higher government revenue and correspondingly higher marginal tax rates, we have to factor in the negative tax multiplier, estimated to be around -1.1. Since the tax multiplier is larger in magnitude than the spending multipliers,22 our estimates imply that GDP declines in response to higher defense spending and correspondingly higher tax revenue. In other words, the estimated balanced-budget multiplier is negative—in the range of -0.3 to -0.7. This result does not accord with simple Keynesian models in which tax multipliers reflect only income effects. But the finding is not surprising in a model where changes in taxes have substitution effects related to marginal income-tax rates.
Samples that start earlier than 1950 show less of an impact from Δτ(-1) on GDP growth; for example, for the sample that starts in 1930, in Table 2, column 3, the estimated coefficient is -0.26 (s.e. = 0.22). One issue is that, during the world wars, GDP may be less responsive than usual to changes in marginal income-tax rates because of extensive governmental controls over the allocation of resources (as discussed later). However, the key influential observation that weakens the estimated tax-rate effect on GDP is the mismatch between the tax-rate cut of 1948 (where the AMTR fell from 0.24 in 1947 to 0.19 in 1948) and the 1949 recession (where per capita real GDP fell by 2.3% for 1948-49). If this one observation is omitted from the 1930 sample (Table 2, column 3), the estimated coefficient Δτ(-1) become -0.52 (s.e. = 0.23), essentially the same as that for the 1950 sample (column 1).23
C. The Yield Spread
Table 2 shows that the estimated coefficient on the yield-spread variable is significantly negative at the 5% level for each sample, except for the one that starts in 1939 (for which the p-value in column 2 is 0.09). The magnitude of the estimated coefficient is similar across samples, except for ones that include the Great Depression. The inclusion of the Depression raises the magnitude of the estimated coefficient (to fit the low growth rates of 1930-33). For example, for the 1930 sample (column 3), if we allow for two separate coefficients on the yield- spread variable, the estimated coefficients are -111.9 (s.e. = 14.7) for 1930-38 and -33.8 (28.6) for 1939-2006. (This regression includes separate intercepts up to and after 1938.) The two estimated coefficients on the yield-spread variable differ significantly with a p-value of 0.021.
An important result is that the estimated coefficients on the defense-spending and tax-rate variables do not change a lot if the equations exclude the yield-spread variable. For example, for the 1939 sample (Table 2, column 2), the estimated coefficients become 0.44 (s.e. = 0.07 Δg: defense, 0.21 (0.07) on defense (-1), 0.045 (0.012) on Δg*: defense news, and -0.19 (0.18) on τ(-1). Similar results apply to the 1930 and 1917 samples. For the 1950 sample (column 1), the deletion of the yield-spread variable raises the magnitudes of the estimated fiscal effects: the estimated coefficients become 0.80 (0.30 on Δg: defense, .08 (0.32) on Δg: defense (-1), 0.034 (0.017) on Δg*: defense news, and -0.63 (0.23) on Δτ(-1).
Since we think that holding fixed a measure of credit conditions sharpens the estimates for the fiscal variables, we focus on the results in Table 2. However, the robustness of the results to deletion of the yield-spread variable heightens our confidence in the estimated fiscal effects.
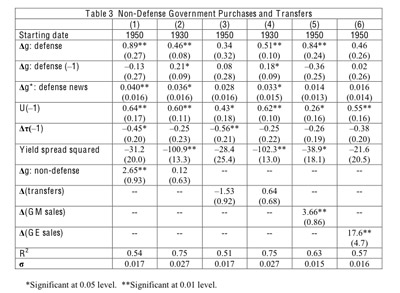
D. Non-Defense Government Purchases
The results in Table 2 seem to provide reliable estimates of defense-spending multipliers, particularly for samples that include WWII. However, to assess typical fiscal-stimulus packages, we are more interested in multipliers for non-defense purchases. The problem, already mentioned, is that this multiplier is hard to estimate because movements in non-defense purchases tend to be endogenous with respect to GDP. Given this problem, it may be helpful to analyze theoretically whether the defense-spending multiplier provides an upper or lower bound for the non-defense multiplier.
One point is that movements in defense spending, driven substantially by war and peace, tend to be more temporary than those in non-defense purchases. For given tax rates, the multiplier is larger when the change in government purchases is more permanent (because the wealth effect is more negative, leading in a market-clearing framework to greater labor supply). On this ground, the multiplier for non-defense purchases likely exceeds that for defense. However, this argument does not apply to the temporary increases in government spending featured in typical stimulus packages.
A related point is that parts of non-defense purchases, such as investments in infrastructure and education, raise future productivity. Therefore, wealth effects for defense purchases tend to be more negative than those for non-defense (a point reinforced by the association of war with enhanced foreign threats). On this ground, the multiplier for defense purchases tends to exceed that for non-defense.
Wars often feature command-and-control techniques, including rationing private expenditure on goods and services, drafting people into the military, and forcing companies to produce tanks rather than cars (all without reliance on explicit prices). Rationing tends to hold down private demand for goods and services, thereby making the spending multiplier smaller than otherwise. However, mandated increases of production and labor tend to raise the multiplier. An offsetting force is that government-mandated output may be under valued in the computation of GDP—if tanks carry unrealistically low "prices" and if draftee wages (including provision of food, housing, etc.) fall short of private-sector wages. Another consideration, stressed by Mulligan (1998), is that, during a popular war such as WWII, patriotism likely shifts labor supply outward, thereby making the wartime multiplier comparatively large.
Overall, our conjecture is that, because of command-and-control and patriotism considerations, the defense-spending multiplier tends to exceed that for non-defense. In this case, the defense-spending multiplier—for which we have good estimates—would provide an upper bound for the non-defense multiplier. However, since the comparison between the multipliers is generally ambiguous on theoretical grounds, it would obviously be desirable to have direct, reliable estimates of the non-defense multiplier.
The key problem, again, is that the principal variations in non-defense purchases are likely to be endogenous with respect to GDP. Columns 1 and 2 of Table 3 show results when we ignore this problem and add a non-defense purchases variable-constructed analogously to the defense variable-to the previous regressions. (We lack a Ramey-type measure of news on non-defense purchases and, therefore, do not include such a variable.) Crucially, the instrument lists include the contemporaneous non-defense purchases variable. The estimated multiplier for the 1950 sample (column 1) is large and significantly different from zero, 2.65 (s.e. = 0.93). However, the estimated coefficient differs insignificantly from zero for longer samples. For example, for the sample starting in 1930, in column 2, the estimated coefficient is 0.12 (0.63).
A plausible reason for the divergent results for the 1950 and 1930 samples is that the endogeneity of non-defense purchases during WWII and the Great Depression differs from that in the post-1950 period. Since 1950, the likely pattern is procyclical: higher GDP generates higher government revenue and thereby induces governments (especially state and local) to spend more. This reverse causation can explain the large estimated multiplier in Table 3, column 1. In contrast, while GDP boomed in WWII, non-defense purchases were crowded out by the added defense spending. During the Great Depression, non-defense purchases rose sharply. Thus, in the 1930s and 1940s, non-defense purchases tended to be counter-cyclical, leading to a small and statistically insignificant estimated multiplier for the post-1930 sample (column 2). In other words, the results for the 1950 and 1930 samples likely reflect different patterns of reverse causation. The estimated coefficients on the non-defense purchases variable in columns 1 and 2 probably have little to do with multipliers, in the sense of the response of GDP to non-defense purchases.
In columns 3 and 4 of Table 3, we replaced the non-defense purchases variable with an analogously defined variable for transfers to persons by all levels of government. Crucially, the instrument lists now include the contemporaneous transfers variable. The endogeneity of transfers with respect to GDP is well-known; for example, unemployment insurance and welfare payments are automatically counter-cyclical. For this reason, the estimated coefficient of the transfers variable in the post-1950 sample is negative: -1.53 (s.e. = 0.92), which has a p-value of 0.10. A reasonable interpretation is that this negative coefficient reflects reverse causation from GDP to transfers, not a negative effect of transfers on GDP. Note that this (familiar) interpretation is analogous to that for non-defense purchases in column 1, except that the reverse causation is positive for non-defense purchases and negative for transfers.
Column 4 of Table 3 shows that the coefficient of the transfers variable changes a lot when we extend the starting date to 1930. Again, this shift likely reflects a different pattern of reverse causation during WWII and the Great Depression, compared to that since 1950.
To illustrate further the potential for spurious estimated multipliers due to endogeneity, columns 5 and 6 of Table 3 replace the non-defense purchases and transfers variables by analogously constructed variables based on sales of two large U.S. corporations with long histories-General Motors and General Electric. The contemporaneous sales variables appear on the instrument list in each case. In column 5, the estimated "multiplier" for GM sales for the 1950 sample is 3.7 (s.e. = 0.9). For GE sales—which are less volatile than GM's but more correlated with GDP—the result is even more extreme, 17.6 (4.7). Moreover, unlike for non-defense purchases and transfers, the estimated GM and GE coefficients do not change a lot when the samples start earlier. Clearly, the estimated coefficients on the GM and GE variables reflect reverse causation from GDP to sales of individual companies. We think that a similar perspective applies for the post-1950 sample in columns 1 and 3 to the apparent multipliers for non-defense purchases and transfers: 2.6 in the first case and -1.5 in the second.
Unfortunately, without good instruments, we cannot estimate multipliers satisfactorily for non-defense government purchases or transfers. This observation has direct policy relevance, because analyses of the U.S. fiscal-stimulus package of 2009 typically use estimated multipliers for government purchases derived from identification schemes analogous to that in column 1 of Table 3. For example, in the large macro-econometric model of Fair (2010, Table 1), which yields a peak multiplier for government purchases of 2.0 at a one-year lag, a key identifying assumption is that variations in non-defense purchases at a quarterly frequency are exogenous with respect to movements in GDP. The rationale is that changes in government purchases entail decision-making lags in the legislative process. However, since private-sector choices of employment, production, and investment also entail lags, it seems unreasonable to regard the contemporaneous association between non-defense purchases and GDP as evidence of effects of the former on the latter, rather than the reverse.
The Congressional Budget Office (2010, appendix) relied on estimated multipliers for government purchases from large macro-econometric models analogous to Fair's: "CBO drew heavily on versions of the commercial forecasting models of two economic consulting firms, Macroeconomic Advisers and Global Insight, as well as on the FRB-US model used at the Federal Reserve Board." The main basis for identification of effects of government purchases in these models is the same as Fair's (2010)—movements in government purchases at a quarterly frequency are treated as exogenous with respect to changes in GDP.24 Based on these estimates, the Congressional Budget Office (2010, Table 2) assumed a range for the peak government-purchases multiplier of 1.0 to 2.5.
Note that the multipliers for government purchases used by Fair (2010, Table 1) and Congressional Budget Office (2010, Table 2) accord with our point estimate of 2.6 for non- defense purchases shown in Table 3, column 1. Thus, the finding of large spending multipliers does not depend on the frequency of the data (quarterly versus annual) or on the use of large models versus a single equation for GDP. The key issue is whether it is satisfactory to use the positive contemporaneous association between non-defense purchases and GDP as evidence for effects of government spending on GDP, rather than the reverse. We think that this identifying assumption is unsatisfactory and tends to generate unrealistically high multipliers—because non-defense purchases are typically procyclical.
Credible estimates of multipliers for non-defense purchases require satisfactory instruments that go beyond arbitrary timing assumptions. One possibility is (exogenous) political variables related to spending programs. Applications of this type include Wright (1974) and Fishback, Horrace, and Kantor (2005) for spending across political jurisdictions by the U.S. government during the New Deal and Johansson (2003) for spending by Swedish municipalities. We are unsure whether this approach will lead eventually to credible estimates of multipliers for non-defense purchases based on data for the United States or other countries.
E. Components of GDP
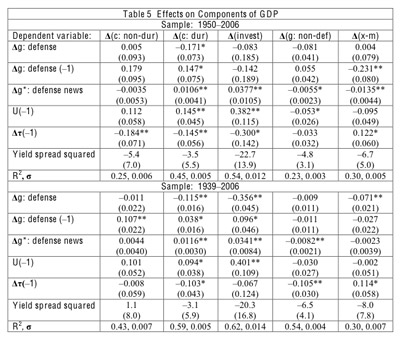
We now assess how changes in defense spending affect components of GDP. We consider the breakdown for GDP net of defense spending into consumption, domestic investment, non-defense government purchases, and net exports. In applications, we identify consumption with consumer expenditure on non-durables and services, and we view consumer spending on durables as a form of investment.
Table 4 summarizes the predictions from the theoretical framework described earlier, expressed as signs for the responses of each component of GDP to changes in current defense spending, g, and news about future defense spending, g*. GDP rises in each case, corresponding to increases in labor input (and, for g, to increased capital utilization). Consumption falls in each case. The declines in non-defense government purchases follow if we view these purchases as primarily forms of consumption. Differing responses show up for domestic investment, which declines in response to higher current spending, g (for given g*), but rises in response to news that future spending will be higher, g* (for given g). The change in net exports, corresponding to the change in net foreign investment, follows the pattern for domestic investment. However, the effects on net exports arise only when the changes in g and g* in the home economy are relative to those in foreign economies.
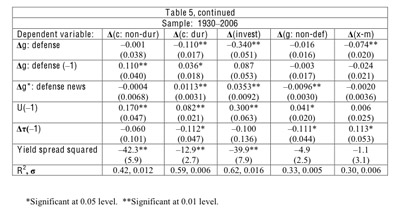
Table 5 shows regressions when the dependent variables are changes in components of GDP. For example, for consumer expenditure on non-durables and services, the dependent variable is the difference between this year's per capita real expenditure (norminal spending) divided by the GDP deflator) and the previous year's per capita all divided by the prior year's per capita real GDP. The same approach applies to consumer expenditure on durables, gross private domestic investment, non-defense government purchases, and net exports. Note that this method relates spending on the various parts of GDP to defense spending and the other right-hand-side variables considered in Table 2 but does not allow for effects from changing relative prices, for example, for consumption goods versus investment goods. In the spending approach, the effects found for overall GDP in Table 2 correspond to the sum of the effects for the components of GDP in Table 5. For example, the defense-spending multiplier estimated in Table 2 equals one plus the sum of the estimated effects on the five components of GDP in Table 5. For the other right-hand-side variables, the estimated effect in Table 2 equals the sum of the estimated effects in Table 5.
The data for the components of GDP in Table 5 come from BEA information available annually since 1929. Therefore, the samples considered do not go back before 1930. (The 1917 sample in Table 2 used non-BEA data before 1929 for GDP and government purchases.)
Consider the 1939 sample, for which the point estimates for the effects on GDP from the contemporaneous defense-spending variables in Table 2, column 2, were 0.44 for Δg: defense and 0.039 for Δg*: defense news. Correspondingly, the effects on the components of GDP in Table 5 add to -0.56 for Δg: defense (contemporaneous crowding out) and 0.039 for Δg*: defense news. The most striking correspondence between the empirical findings and the theory (Table 4) is for the impact of the current defense-spending variable on investment. The estimated coefficients for Δg: defense for the 1939 sample in Table 5 are significantly negative: -0.115 (s.e. = 0.016) for durable consumption purchases and -0.356 (0.045) for gross private domestic investment, whereas those for Δg*: defense news are significantly positive: 0.012 (0.003) and 0.034 (0.008), respectively. The theory predicted negative effects on consumption, but the estimated effects from the current defense-spending variables on non-durable consumer spending differ insignificantly from zero. For non-defense government purchases, the estimated effect from Δg: defense also differs insignificantly from zero, but that from Δg*: defense news is significantly negative, -0.008 (0.002), as predicted. Finally, for net exports, the estimated effect from Δg: defense is significantly negative, -0.07 (0.02), as expected, but that from Δg*: defense news differs insignificantly from zero. The last effect may arise because changes during the major wars in U.S. g* tend to go along with corresponding changes in many countries' g*.
The results for Δg: defense and Δg*: defense news in Table 5 for the other samples are similar, except that the standard errors are higher for the 1950 sample. One difference is that the effect of Δg*: defense news on net exports in the 1950 sample is significantly negative, -0.014 (s.e. = 0.004).
The negative effect from the average marginal income-tax rate on GDP shows up most clearly in Table 2 for the 1950 sample, with an estimated coefficient of -0.54 (s.e. = 0.21). Table 5 shows that this response shows up across the board for the categories of consumer spending and investment: -0.18 (0.07) for non-durable consumer expenditure, -0.14 (0.06) for durable consumer expenditure, and -0.30 (0.14) for gross private domestic investment.
For the yield-spread variable, Table 2 shows negative effects on GDP for all samples, but the response is larger in size and more statistically significant in the 1930 sample. In Table 5, the negative effects for the 1930 sample are spread across non-durable consumer spending, -42.3 (s.e. = 5.9), durable consumer spending, -12.9 (2.7), and gross private domestic investment, -39.9 (7.9).
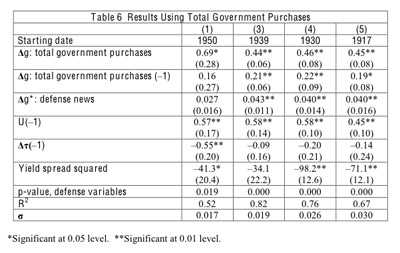
F. Total Government Purchases
If an expansion of defense spending crowds out non-defense purchases, the rise in overall government purchases would fall short of the increase in defense spending. Therefore, a multiplier calculated from defense spending alone may understate the multiplier computed for overall government purchases. If we assume that the non-defense and defense multipliers are the same,25 we can estimate the multiplier for overall purchases by replacing the variable Δg: defense in Table 2 with, Δg:: total government purchases, computed from overall government purchases. In these revised equations, shown in Table 6, the instrument list still includes the variable Δg: defense, not Δg: total government purchases. However, the lagged value of Δg: total government purchases is on the instrument list.
If we compare the results from Table 6 with those from Table 2, we find little changes in the estimated effects when comparing the coefficients of Δg: total government purchases (contemporaneous and lagged) with those for Δg: defense. The reason is that, in Table 5, the crowding-out effects from Δg: defense (contemporaneous and lagged) on non-defense government purchases are small and statistically insignificantly different from zero. The significant crowding-out applies to the variable Δg*: defense news. Because of this channel, the estimated effects from Δg*: defense news on GDP are somewhat higher—by around 0.005 in the longer samples—in Table 6 than in Table 2. The bottom line is that the shift to total government purchases produces only minor changes in the estimated spending multipliers.
G. More Results on Taxes
Thus far, the findings on taxes involve changes in average marginal income-tax rates, which have straightforward substitution effects. However, tax changes may also matter through wealth effects, the channel stressed by Romer and Romer (2009). These effects would involve changes in tax revenue, rather than marginal tax rates.
Empirically, movements in the average marginal income-tax rate, AMTR, are substantially positively correlated with changes in tax revenue. From 1950 to 2006, the correlation of the change in the federal part of our AMTR is 0.62 with the change in per capita real federal revenue expressed as a ratio to the prior year's per capita real GDP, 0.74 with the variable that Romer and Romer (2008) constructed to gauge incremental federal tax revenue (expressed as a ratio to lagged GDP), and 0.46 with the part of their incremental federal revenue that Romer and Romer labeled as exogenous (expressed relative to lagged GDP). Given these correlations, the AMTR used in Table 2 could be picking up a combination of substitution and wealth effects in the determination of GDP. We try now to sort out these effects.
Table 7 presents further results on taxes for the 1950-2006 sample. Column 1 is the same as column 1 of Table 2, except for a minor difference in the instrument list. As before, the estimated coefficient on the first lag of the change in the AMTR is significantly negative, -0.53 (s.e. = 0.21).26 If we add an additional lag of the change in the AMTR, the estimated coefficient on the first lag changes little, and that on the second lag is statistically insignificantly different from zero, -0.22 (0.22).
Column 2 of Table 7 replaces the AMTR variable by the first lag of the variable emphasized by Romer and Romer (2009)—the exogenous part of intended changes in federal tax revenue expressed as a ratio to lagged GDP. This variable appears also on the instrument lists for all of the regressions shown in the table. The estimated coefficient of the lagged Romer-Romer variable is negative, -1.08 (s.e. = 0.57), but statistically significant only with a p-value of 0.06.27 If we add an additional lag, the estimated coefficient on the first lag changes little, and that on the second lag is statistically insignificantly different from zero, -0.48 (0.55). This timing—the principal negative effect appearing with a one-year lag—is broadly consistent with the results of Romer and Romer (2009, Figure 5) using quarterly data.
Column 3 of Table 7 includes simultaneously the first lags of the changes in the AMTR and the Romer-Romer exogenous tax-change variable. The estimated coefficient of the AMTR variable, -0.43 (s.e. = 0.24), is significantly negative with a p-value of 0.07, and that on the Romer-Romer variable, -0.56 (0.62), differs insignificantly from zero. The two variables are jointly significant with a p-value of 0.029.
As mentioned before, the problem with estimating contemporaneous effects of tax variables is endogeneity. If we add the current year's change in the AMTR to the equation in Table 7, column 1, and also include this variable on the instrument list, we get that the estimated coefficient on the current change has the "wrong" sign, 0.39 (s.e. = 0.24), whereas that on the lagged change is still significantly negative, -0.68 (0.23). The positive coefficient on the contemporaneous change likely reflects the endogenous determination of the AMTR. If we modify the instrument list to replace the current change in AMTR by the change based on the current year's tax law and the prior year's incomes,28 the estimated coefficients do not change much: 0.36 (0.30) on the current change and -0.67 (0.24) on the lag. The likely problem is that this instrument still leaves the endogeneity associated with legislated changes in the tax structure.
Column 4 of Table 7 includes the contemporaneous and lagged AMTR changes in the equation and adds as an instrument the contemporaneous Romer-Romer exogenous tax-change variable.29 The estimated coefficients on the AMTR variables are 0.12 (s.e. = 0.47) on the contemporaneous value and -0.58 (0.28) on the lag. The near-zero coefficient on the contemporaneous variable likely arises because the Romer-Romer variable eliminates much, but perhaps not all, of the endogenous legislative response. In any event, we still find a significantly negative effect from the change in the AMTR only with a one-year lag. Column 5 of the table shows that the estimated coefficient of the contemporaneous tax change is also close to zero when the equation includes the current and lagged values of the Romer-Romer variable, rather than the AMTR variable.
Since the spirit of the Romer-Romer analysis is to look for income effects from federal-tax changes, it seems appropriate not to include their variable directly in the GDP equation but rather to include the change in overall federal revenue and then use their exogenous tax-change measure as an instrument. Column 6 of Table 7 includes the first lag of the change in a variable based on total federal revenue (the change in per capita real federal revenue expressed as a ratio to the previous year's per capita real GDP). This form implies that the coefficient on the federal-revenue variable directly reveals the "tax multiplier." The estimated coefficient, -0.46 (s.e. = 0.27), is negative but statistically significantly different from zero only with a p-value of 0.09. If we add a second lag of the federal-revenue variable, the estimated coefficient of the first lag changes little, and that on the second lag is close to zero, 0.03 (0.27).
Column 7 of Table 7 includes simultaneously the first lags of the changes in the AMTR and the federal-revenue variable. In this specification, the estimated coefficient of the AMTR variable, -0.45 (s.e. = 0.24), is significantly negative with a p-value of 0.07, whereas that on the federal-revenue variable, -0.17 (0.30), differs insignificantly from zero. Thus, the results prefer the AMTR variable to the measure of federal revenue.
We also estimated equations that include the contemporaneous change in the federal- revenue variable, while including the contemporaneous Romer-Romer exogenous tax-change variable as an instrument. If we add these variables to the specification in Table 7, column 6, the estimated coefficients are 0.74 (s.e. = 0.51) on the contemporaneous federal-revenue variable and -0.51 (0.22) on the lagged value. These variables are jointly significant with a p-value of 0.04. However, if we reinsert the lagged change in the AMTR into the equation, we get a significantly negative coefficient on this variable, -0.42 (0.21), and an insignificant effect from the lagged federal-revenue variable, -0.23 (0.26). Therefore, the lagged federal-revenue variable seems just to have been proxying for the lagged change in the AMTR. If we eliminate the lagged federal-revenue variable, as in column 8 of Table 7, we get the usual significantly negative coefficient on the lagged AMTR, -0.52 (0.18), and a positive but statistically insignificant coefficient on the contemporaneous federal-revenue variable, 0.46 (0.53). A positive coefficient on the contemporaneous change in federal tax revenue (if it were statistically significant) could be interpreted in terms of wealth effects—lower wealth from higher anticipated future government spending spurring greater work effort.
The bottom line is that the post-1950 U.S. data provide evidence for a negative effect of increases in the average marginal income-tax rate, AMTR, on GDP. These effects show up mostly with a one-year lag. Once we hold constant the lagged change in the AMTR, we find no statistically significant effects from variables that reflect exogenous changes in federal tax revenue and are, therefore, likely to pick up wealth effects. In contrast, with the revenue variables included, the lagged change in the AMTR still has at least a marginally significant negative effect on GDP. We conclude from this limited evidence that the main effects from tax changes on GDP may involve substitution effects, rather than wealth effects.
VII. Concluding Observations
For samples that include WWII, the estimated multiplier for temporary defense spending is 0.4-0.5 contemporaneously and 0.6-0.7 over two years. If the change in defense spending is "permanent" (gauged by Ramey's defense-news variable), the multipliers are higher by 0.1-0.2. These multipliers are all significantly less than one and apply for given average marginal income-tax rates. In contrast, we lack reliable estimates of multipliers for non-defense purchases, because the lack of good instruments makes it infeasible to isolate the direction of causation between these purchases and GDP.
Since the estimated defense-spending multiplier is less than one, a rise in defense spending is estimated to crowd out other components of GDP. The main crowding-out applies to investment, broadly defined to include purchases of consumer durables, but negative effects show up also for net exports. In contrast, a permanent increase in defense spending has less of a negative effect on investment but significantly depresses non-defense government purchases. Estimated effects of temporary or permanent defense spending on consumer expenditure on non-durables and services are small and statistically insignificantly different from zero.
The post-1950 sample reveals significantly negative effects on GDP from increases in the average marginal income-tax rate, AMTR. When interpreted as a tax multiplier (using the historical association between changes in federal revenue and changes in the AMTR), the value is around -1.1. However, these tax-rate effects are less reliably estimated in long samples. Once we hold constant the behavior of the AMTR, we find no statistically significant effects on GDP in the post-1950 sample from "exogenous" movements in federal revenue (using the Romer-Romer exogenous federal tax change). In contrast, when revenue is held constant, we still find at least marginally significant negative effects on GDP from increases in the AMTR. Thus, changes in taxes may influence GDP mainly through substitution effects, rather than wealth effects.
If higher defense spending goes along with higher federal revenue and correspondingly higher marginal tax rates, we have to factor in the negative tax multiplier, estimated to be around -1.1. Since the estimated expenditure multipliers for given tax rates were significantly less than one, the full effect from greater defense spending and correspondingly higher taxes is to reduce GDP; that is, the estimated balanced-budget multiplier is negative.
We are presently trying to apply the methodology to long-term macroeconomic data for other countries.30 However, the approach works well for the United States because the main wars involved dramatic, exogenous variations in defense outlays but little destruction of domestic capital stock and only moderate loss of American life. The devastation in many other countries during the world wars would preclude a similar analysis; that is, adverse supply shocks would confound the demand effects from greater government spending.
Promising cases that seem analogous to the U.S. experience are Australia, Canada, New Zealand, and South Africa. These cases are especially interesting because the entry dates into the world wars, 1914 and 1939, precede the U.S. dates. In particular, the earlier entry into WWII means that dramatic increases in defense spending occurred when unemployment rates were particularly high—for Canada, the sharp rise in defense spending in 1940 matches up with an unemployment rate of 14.1% in 1939. Therefore, the four countries should provide clearer evidence about whether the defense-spending multiplier interacts with the amount of slack in the economy. However, further research is necessary to assess the feasibility of constructing time series for these countries on defense news and average marginal income-tax rates. These variables featured prominently in our study for the United States.
ENDNOTES
1. Standard numbers for real government purchases use a government-purchases deflator that assumes zero productivity change for inputs bought by the government. We proceed instead by dividing nominal government purchases by the GDP deflator, effectively assuming that productivity advance is the same for publicly purchased inputs as it is in the private economy.
2. The data since 1929 are the BEA's "government consumption and gross investment." This series includes an estimate of depreciation of public capital stocks (a measure of the rental income on publicly owned capital, assuming a real rate of return of zero on this capital).
3. The current federal individual income-tax system was implemented in 1913, following the ratification of the 16th Amendment, but the first detailed publication from the IRS applies mostly to 1916. We use IRS information from the 1916 book on tax-rate structure and numbers of returns filed in various income categories in 1914-15 to estimate average marginal income-tax rates for 1914 and 1915. For 1913, we approximate based on tax-rate structure and total taxes paid.
4.The constructed AMTR considers the impact of extra income on the EITC, which has become a major transfer program. However, the construct does not consider effects at the margin on eligibility for other transfer programs, such as Medicaid, food stamps, and so on.
5. The Barro-Sahasakul federal marginal tax rate does not consider the deductibility of part of state income taxes. However, since the average marginal tax rate from state income taxes up to 1965 does not exceed 0.016, this effect would be minor. In addition, the Barro-Sahasakul series treats the exclusion of employer social-security payments from taxable income as a subtraction from the social-security rate, rather than from the marginal rate on the federal income tax. However, this difference would not affect the sum of the marginal tax rates from the federal income tax and social security.
6. The first state income tax was implemented by Wisconsin in 1911, followed by Mississippi in 1912. A number of other states (Oklahoma, Massachusetts, Delaware, Missouri, New York, and North Dakota) implemented an income tax soon after the federal individual income tax became effective in 1913.
7. Before 1929, we do not have the BEA data on income by state. For this period, we estimated the average marginal tax rate from state income taxes by a linear interpolation from 0 in 1910 (prior to the implementation of the first income tax by Wisconsin in 1911) to 0.0009 in 1929. Since the average marginal tax rates from state income taxes are extremely low before 1929, this approximation would not have much effect on our results.
8. Conceptually, our "marginal rates" correspond to the effect of an additional dollar of income on the amounts paid of the three types of taxes. The calculations consider interactions across the levies; for example, part of state income taxes is deductible on federal tax returns, and the employer part of social-security payments does not appear in the taxable income of employees.
9. However, the tax-rate structure need not be set at the beginning of year t. Moreover, for a given structure, information about a household's marginal income-tax rate for year t arrives gradually during the year as the household learns about its income, deductions, etc.
10. A major counter-example is the Reagan tax cut of 1986, which reduced the average marginal tax rate from the federal individual income tax by 4.2 percentage points up to 1988. Because this program was designed to be revenue neutral (by closing "loopholes" along with lowering rates), the Romer-Romer variable shows only minor federal tax changes in 1987 and 1988.
11.Ricardian equivalence does not necessarily imply that these effects are nil. A high value of the Romer-Romer tax variable might signal an increase in the ratio of expected future government spending to GDP, thereby likely implying a negative wealth effect.
12. For a given ratio of federal revenue to GDP, an increase in the AMTR might signal that the government had shifted toward a less efficient tax-collection system, thereby implying a negative wealth effect.
13. The first bin does not actually involve endogeneity of tax changes with respect to GDP but instead reflects concern about a correlated, omitted variable—government spending—that may affect GDP. Empirically, the main cases of this type in the Romer-Romer sample associate with variations in defense outlays during and after wars, particularly the Korean War.
14. Note that the variable yt is the per capita value of nominal GDP divided by the implicit GDP deflator, Pt (determined by the BEA from chain-weighting for 1929-2006). The variable gt is calculated analogously as the per capita value of government purchases (such as defense spending) divided by the same Pt. Therefore, the units of y and g are comparable and β1 reveals the effect of an extra unit of government purchases on GDP.
15. Romer and Romer (2008, Table 1, columns 9-12) estimate the implications of tax legislation for the projected present value of federal revenue, and these changes can be distinguished from the effects for the initial year (columns 1-4). However, we find empirically (in accord with Romer and Romer [2009, Section VI]) that the present-value measure consistently lacks significant incremental explanatory power for GDP.
16. Since the yield spread has strong persistence, the lagged value has high explanatory power. For example, in a first-stage regression for the square of the yield spread from 1917 to 2006, the t-statistic on the lagged variable is 9.3.
17. See Barro (1984, pp. 312-315) for an earlier analysis of the effects of wartime spending on output. Hall (2010, Table 1) also presents estimates of defense-spending multipliers associated with wars.
18. A sample starting in 1914 gives results similar to those for the 1917 sample shown in Table 2, column 5. Given the large measurement error in the variable Δg*: defense news for 1914-16, we do not present the results for the 1914 sample.
19. If we add the lagged value of Δg*: defense news, the estimated coefficient is close to zero.
20. We treated as major wars WWI, WWII, the Korean War, and the Vietnam War, including a year of war aftermath for each case. The specific sample is 1914-20, 1939-46, 1950-54, and 1966-71. We treated WWI as ending in 1919 (because of continuing conflicts after the 1918 Armistice involving Russia, Poland, Greece, Turkey, and other countries) and thereby included 1920 as the year of war aftermath. However, the results change little if we treat the war as ending in 1918, so that 1919 is the year of war aftermath.
21. This result is not surprising because, in a first-stage regression for 1939-206 of Δg: defense on the "exogenous" variables, the estimated coefficient on Δg: defense interacted with war years is 0.945 (s.e. = 0.012); that is, the t-statistic is 77.
22. This result accords with Alesina and Ardagna (2010), who study 107 cases of large fiscal contraction and 91 of large fiscal stimulus for 21 OECD countries from 1970 to 2007. They find that fiscal stimuli are more likely to increase economic growth when the package is concentrated more on tax cuts than on spending increases. Similarly, they find for fiscal contractions that recessions are more likely to materialize when the package focuses on tax increases rather than spending reductions.
23. The cut by 4.6 percentage points in 1948 in the average marginal income-tax rate from the federal individual income tax is the largest one-year decline over the entire sample. This reduction reflected two changes with roughly equal effects on the AMTR: the introduction of a much more favorable treatment for joint returns (taxing a couple's income as though each spouse were a single person with half the family income) and the shift to a more generous tax-computation formula that cut the schedule of marginal tax rates for all taxpayers. Political events may have exerted important effects on expectations about tax-rate changes between 1947 and 1949. The underlying legislation passed in April 1948 when the heavily Republican Congress overrode President Truman's veto. Similar legislation passed the Congress twice in 1947, but Truman's veto was barely sustained in each case (see Romer and Romer [2008, p. 20]) and Thorndike [2006]). Given this background, the usual time pattern—whereby tax-rate cuts have their main effect on GDP with a one-year lag—may not apply. That is, the belief in 1947 that major tax-rate cuts were coming might have accelerated the response of GDP to the tax-rate cuts. A related idea is that the surprise reelection of Truman in 1948 and the accompanying shift back to a Democratic Congress would have affected expectations of tax-rate changes in 1949. The broader suggestion is that exogenous political events might affect GDP by influencing expectations of tax-rate changes.
24. The vector-autoregression (VAR) literature typically makes the same identifying assumption: changes in government purchases are pre-determined within a quarter; see, for example, Blanchard and Perotti (2002). Communications from IHS Global Insight indicate that they treat changes in federal non-defense purchases as exogenous but state & local purchases as dependent on state & local tax revenue and federal transfers.
25. We cannot test this proposition without satisfactory instruments related to non-defense purchases.
26. Our focus is on the overall marginal income-tax rate; that is, we implicitly have the same coefficients for changes in federal and state income-tax rates as for changes in social-security tax rates. If we separate the two income-tax rates from the social-security rate, we surprisingly get larger size coefficients for social security. The hypothesis of equal magnitude coefficients for the two variables is rejected with a p-value of 0.009. We have no good explanation for this result. However, a key part of the data pattern is that the increases in the AMTR from social security starting in the early 1970s fit well with the recessions of the mid 1970s and early 1980s.
27. The estimated coefficient becomes significantly negative at the 0.05 level, -1.11 (s.e. = 0.47), if we enter instead the lagged value of the Romer-Romer intended change in overall federal tax revenue, with the exogenous part still on the instrument list.
28. We constructed this variable, using the NBER's TAXSIM program, for the federal individual income tax and social security from 1967 to 2006. We formed an instrument by taking the AMTR computed from the current tax law and the prior year's incomes for the federal income tax and social security and subtracting the actual AMTR for these taxes from the previous year. (This procedure assumes a value of zero for the change in the AMTR from state income taxes.) For 1950-66, the instrument takes on the constant value -0.0005, which is the median change from 1950 to 2006. In a regression for 1950-2006 of the change in the AMTR on all of the instruments, the estimated coefficient on the newly constructed variable is 1.05 (s.e. = 0.11), with a t-statistic of 9.2. The F-statistic for the four excluded instruments is 24. Therefore, weak instruments are not a problem here.
29. In a regression for 1950-2006 of the change in the AMTR on all of the instruments, the estimated coefficient on the contemporaneous Romer-Romer variable is 1.05 (s.e. = 0.31), implying a t-statistic of 3.4. The F-statistic for the four excluded instruments is 4.2, indicating that weak instruments might be a problem here.
30. Almunia, et al. (2010) provide suggestive evidence that defense-spending multipliers are positive in a panel of 27 countries for 1925-1939. The results (in their Table 2) are hard to interpret because the measures of government expenditure include transfers and interest payments and lack a consistent definition across countries in terms of central versus total government.
REFERENCES
Aiyagari, R., A. Marcet, T. Sargent, and J. Seppala (2002). "Optimal Taxation without State-Contingent Debt," Journal of Political Economy, 110, December, 1220-1254.
Alesina, A. and S Ardagna (2010). "Large Changes in Fiscal Policy: Taxes versus Spending," Tax Policy and the Economy, 24, forthcoming.
Almunia, M., A. Benetrix, B. Eichengreen, K.H. O'Rourke, and G. Rua (2010). "From Great Depression to Great Credit Crisis: Similarities, Differences, and Lessons," Economic Policy, 25, forthcoming.
Balke, N.S. and R.J. Gordon (1989). "The Estimation of Prewar Gross National Product: Methodology and New Evidence," Journal of Political Economy, 97, February, 38-92.
Barro, R.J. (1979). "On the Determination of the Public Debt," Journal of Political Economy, 87, October, 940-971.
Barro, R.J. (1984). Macroeconomics, New York, Wiley.
Barro, R.J. and R.G. King (1984). "Time-Seperable Preferences and Intertemporal-Substitution Models of Business Cycles," Quarterly Journal of Economics, 99, November, 817-839.
Barro, R.J. and C. Sahasakul (1983). "Measuring the Average Marginal Tax Rate from the Individual Income Tax," Journal of Business, 56, October, 419-452.
Barro, R.J. and C. Sahasakul (1986). "Average Marginal Tax Rates from Social Security and the Individual Income Tax," Journal of Business, 59, October, 555-566.
Barro, R.J. and J.F. Ursua (2008). "Consumption Disasters since 1870," Brookings Papers on Economics Activity, spring, 255-335.
Blanchard, O. and R. Perotti (2002). "An Empirical Characterization of the Dynamic Effects of Changes in Government Spending and Taxes on Output," Quarterly Journal of Economics, 117, November, 1329-1368.
Chetty, R. (2009). "Bounds on Elasticities with Optimization Frictions: A synthesis of Micro and Macro Evidence on Labor Supply," National Bureau of Economic Research working paper no. 15616, December.
Congressional Budget Office (2010). "Estimated Impact of the American Recovery and Reinvestment Act on Employment and Economic Output from October 2009 through December 2009," Washington DC, February.
Darby, M.R. (1976). "Three-and-a-Half Million U.S. Employees Have Been Mislaid: Or an Explanation of Unemployment, 1934-1941," Journal of Political Economy, 84, February, 1-16.
Fair, R.C. (2010). "Estimated Macroeconomic Effects of the U.S. Stimulus Bill," unpublished, Yale University, March.
Fishback, P.V., W.C. Horrace, and S. Kantor (2005). "Did New Deal Grant Programs Stimulate Local Economies? A Study of Federal Grants and Retail Sales during the Great Depression," Journal of Economic History, 65, March, 36-71.
Gilchrist, S., V. Yankov, and E. Zakrajsek (2009). "Credit Market Shocks and Economic Fluctuations: Evidence from Corporate Bond and Stock Markets," Journal of Monetary Economics, 56, May, 471-493.
Hall, R.E. (2010). "By How Much Does GDP Rise if the Government Buys More Output?" Brookings Papers on Economic Activity, forthcoming.
Johansson, E. (2003). "Intergovernmental Grants as a Tactical Instrument: Empirical Evidence from Swedish Municipalities," Journal of Public Economics, 87, May, 883-915.
Kendrick, J.W. (1961). Productivity Trends in the United States, Princeton NJ, Princeton University Press.
Mulligan, C.B. (1998). "Pecuniary Incentives to Work in the United States during World War II," Journal of Political Economy, 106, October, 1033-1077.
Ramey, V.A. (2009a). "Identifying Government Spending Shocks: It's All in the Timing," unpublished, University of California San Diego, October.
Ramey, V.A. (2009b). "Defense News Shocks, 1939-2008: Estimates Based on News Sources," unpublished, University of California San Diego, October.
Redlick, C.J. (2009). Average Marginal Tax Rates in the United States: A New Empirical Study of their Predictability and Macroeconomic Effects, 1913-2006, unpublished undergraduate thesis, Harvard University.
Romer, C.D. (1986). "Spurious Volatility in Historical Unemployment Data," Journal of Political Economy, 94, February, 1-37.
Romer, C.D. and D.H. Romer (2008). "A Narrative Analysis of Postwar Tax Changes," unpublished, University of California Berkeley, November.
Romer, C.D. and D.H. Romer (2009). "The Macroeconomic Effects of Tax Changes: Estimates Based on a New Measure of Fiscal Shocks," unpublished, University of California Berkeley, April, forthcoming in American Economic Review.
Stock, J.H. and M.W. Watson (2003). "Forecasting Output and Inflation: The Role of Asset Prices," Journal of Economic Literature, 41, September, 788-829.
Thorndike, J.J. (2006). "Out of (Re)alignment: Taxes and the Election of 1946," Tax History Project, available on the Internet at www.taxhistory.org, December 14.
Wright, G. (1974). "The Political Economy of New Deal Spending: An Econometric Analysis," The Review of Economics and Statistics, 56, February, 30-38.
Note: See the text on the construction of average (income-weighted) marginal tax rates for the federal individual income tax, social-security payroll tax, and state income taxes. Values shown in brackets for state income taxes for 1912-28 are interpolations. The total is the sum of the three pieces. The construction of these data is detailed in an appendix posted at http://www.economics.harvard.edu/faculty/barro/data_sets_barro.
Notes to Table 2 Data are annual from the starting year shown through 2006. The dependent variable is the change from the previous year in per capita real GDP divided by the previous year's per capita real GDP. Data on per capita real GDP are from Barro and Ursua (2008), who use BEA (Bureau of Economic Analysis) data since 1929 and pre-1929 information from Balke and Gordon (1989). The underlying population numbers include U.S. military overseas. Δg: defense is the change from the previous year in per capita real defense spending (nominal spending divided by the GDP deflator) divided by the previous year's per capita real GDP. Data since 1929 on defense outlays are from BEA, and pre-1929 data are from Kendrick (1961). The lagged value of this variable, Δg: defense (-1), is also included. Δg*: defense news is from Ramey (2009a, Table 2; 2009b), who uses news sources to estimate the present discounted nominal value of expected changes in defense spending applying in most cases over the next three to five years. Her data were expressed as ratios to the prior year's nominal GDP. Data since 1929 on U, the unemployment rate, are from BLS (Bureau of Labor Statistics). We adjusted the BLS numbers from 1933 to 1943 to classify federal emergency workers as employed, as discussed in Darby (1976). Values before 1929 are from Romer (1986, Table 9). Δτ is the change from the previous year in the average marginal income-tax rate from federal and state income taxes and social security, as shown in Table 1. The yield spread is the difference between the yield on long-term Baa corporate bonds and that on long-term U.S. Treasury bonds. Before 1919, the spread is estimated from data on long-term Aaa corporate bonds. The square of the spread appears in the equations. Data on yields are from Moody's, as reported on the website of the Federal Reserve Bank of St. Louis.
Estimation is by two-stage least-squares, using as instruments all of the independent variables in this table, except for the square of the yield spread, which is replaced by its lagged value. The instrument list also contains the first lag of the dependent variable. The p-value is for a test that the coefficients are all zero for the three variables related to defense spending.
Note: See the notes to Table 2. The first two columns include the variable Δg: non-defense, the change from the previous year in per capita real non-defense government purchases (nominal purchases by all levels of government divided by the GDP deflator), divided by the previous year's per catpia real GDP. The variable Δg: non-defense is included in the instrument lists for these columns. The next two columns include the variable Δ(transfers), which is the change in per capita real government transfers to persons (nominal transfers by all levels of government divided by the GDP deflator), divided by the previous year's per catpia real GDP. The variable Δ(transfers) is included in the instrument lists for these columns. Data since 1929 on non-defense government purchases and transfers are from Bureau of Economic Analysis. Δ(GM sales) is the change from the previous year in per capita real net sales of General Motors Corporation, express as a ratio to the previous year's per capita real GDP. Real net sales are nominal sales divided by the GDP deflator. This variable is included in the instrument list for column 5. Δ(GE sales), in column 6, is treated analogously, based on net sales of General Electric Corporation. The GM and GE data come from annual reports of the two companies.
Note: The table considers in the left-most column increases in current defense spending, g, or in news about future defense spending, g*. The five columns to the right show the signs of the predicted changes in GDP and its four components: private consumption, gross private domestic investment, non-defense government purchases, and net exports. The effects on non-defense government purchases follow if we view these purchases as primarily consumption, rather than investment. In our empirical application, we identify consumption with personal consumer expenditure on non-durables and services, and we consider consumer expenditure on durables as a form of investment.
Notes: These results correspond to Table 2, except for the specifications of the dependent variables, which are now based on components of GDP. For the non-durables and services part of personal consumer expenditure, Δ(c:non-dur), the dependent variable equals the change in per capita real expenditure (nominal expenditures divided by the GDP deflator), expressed as a ratio to the previous year's per capita real GDP. The same approach applies to purchases of consumer durables, Δc:(dur), gross private domestic investment, Δ(invest), non-defense government purchases by all levels of government, Δ(g: non-def), and net exports, Δ(x-m). Data since 1929 are from the Bureau of Economic Analysis.
Note: These results correspond to Table 2, except that the variable Δg now refers to total government purchases, rather than defense outlays. The instruments are the same as those used in Table 2, except that the lagged change in total government purchases appears instead of the lagged change in defense spending.
Note: See notes to Table 2. Data are annual 1950-2006. Columns 1,3,4,7,8 include the lag of the change in the average marginal income-tax rate, τ. Column 4 adds the contemporaneous Δτ. Columns 2,3,5 include the lag of the Romer and Romer (2008, Table 1, columns 1-4) exogenous tax-change variable, described in the text. Column 5 adds the contemporaneous value of this variable. Columns 6 and 7 include the lagged value of Δ(federal taxes)/Y(-1), the change in per capita real federal revenue (total nominal receipts from BEA divided by the GDP deflator), expressed as a ratio to the previous year's per capita real GDP. Column 8 has the contemporaneous value of this variable. The instrument list for all equations includes Δg: defense, Δg: defense(-1), Δg*: defense news, U(-1), Δτ(-1), the first lages of the dependent variable and the square of the yield spread, and the first lage of the Romer-Romer exogenous tax-change variable. Columns 4,5,8 add the contemporaneous Romer-Romer variable. Columns 6, 7, 8 and the lagged change in the federal-revenue variable.
Note: The figure shows the change in per capita real government purchases (nominal purchases divided by the GDP deflator), expressed as a ratio to the prior year's per capita real GDP. The blue graph is for defense purchases, and the red graph is for non-defense purchases by all levels of government. The data on government purchases since 1929 are from Bureau of Economic Analysis and, before that, from Kendrick (1961). The GDP data are described at http://www.economics.harvard.edu/faculty/barro/data_sets_barro.
Note: From 1939 to 2008, the variable is the annual counter-part of Ramey's (2009a, Table 2) measure of the present value of expected future nominal defense spending, expressed as a ratio to the prior year's nominal GDP. Values from 1913 to 1938 are rough estimates, described in section II of the text. We use the defense-news variable to measure (g*t - g*t-1)/yt-1 in equation (1) in section V of the text.
Note: The red graph is for the federal individual income tax, the green graph for the social- security payroll tax (FICA), and the black graph for state income taxes. The blue graph is the total average marginal income-tax rate. The data are from Table 1.